The past two decades have seen exponential growth in the burgeoning field of unmanned systems, foretelling what may one day be viewed as the biggest paradigm shift in the evolution of mankind. Military drones have forever changed the conduct of war, providing persistent surveillance, enhanced command and control, and precision strike capabilities, while ground robots play life-saving roles in neutralizing landmines and improvised explosive devices. On the civilian side, self-driving cars, trucks, buses, and even bicycles are no longer wishful fantasy, already mingling with manned vehicles on congested roadways. Thousands of autonomous material-handling robots work tirelessly around the clock, fetching millions of products in Amazon’s massive fulfillment warehouses, with airborne and street-level drones already envisioned for doorstep delivery. These are indeed exciting times!
Contrary to popular belief, however, interest in robots and drones dates back long before most people realize, as the United States and other countries have been employing unmanned military systems for more than a century. One of the earliest attempts at airborne force projection, for example, involved free-flight balloons introduced during Austria’s 1849 siege of Venice during the Italian War of Independence. Each of these 23-foot-diameter balloons trailed a long copper wire that remotely triggered the release of a bomb over target.
As supporting technologies evolved, a number of wirelessly directed airships appeared, such as the 22-foot dirigible of inventor Albert Leo Stevens and electrical engineer Mark O. Anthony, who put on a two-hour demonstration at a blimp hangar in Hoboken, NJ, in February 1909. The following year, Raymond Phillips demonstrated a 20-foot model of a Zeppelin dirigible inside the London Hippodrome, astonishing his audience with aerial maneuvers and flashing lights. New Zealand inventor Alban J. Roberts developed a similar radio-controlled model for theatric performances in 1912 (Figure 1). Another model airship, built by Christopher Wirth of Nuremburg, Germany, was demonstrated at a Berlin circus in 1913.
Figure 1. New Zealand inventor Alban J. Roberts stands behind the wireless controller for his 15-foot dirigible during an indoor demonstration in 1912.
The inherent stability of these lighter-than-air systems relative to primitive fixed-wing aircraft of the time provided a distinct advantage for remote control, but their susceptibility to ambient air currents made the battery-powered craft impractical for outdoor operation. This issue, plus their relatively short battery life and the range limitations of early wireless gear, meant that demonstrations were confined to indoor venues, and thus ill-suited for military use. Several attempts to remotely operate full-size airships powered by gasoline engines ensued, but were found to be more or less impractical.
Years later during WWII, Japan took an entirely different approach, purposely electing to harness the power of reasonably predictable winds aloft for sustained propulsion over long distances, without the need for radio control. Military engineers reasoned that the 200-mph winter jet stream, about which the rest of the world knew very little, could theoretically push at least 10 percent of their weaponized free-flight balloons across the Pacific Ocean in about 3 days. A sustained attack against North America began in November, 1944, during which some 9300 incendiary Fu-Go balloons were launched (Figure 2), of which an estimated 900 to 1000 crossed the Pacific and made landfall. While there were 361 confirmed arrivals in the United States and Canada, the winter rainy season substantially reduced the threat of wildfires.
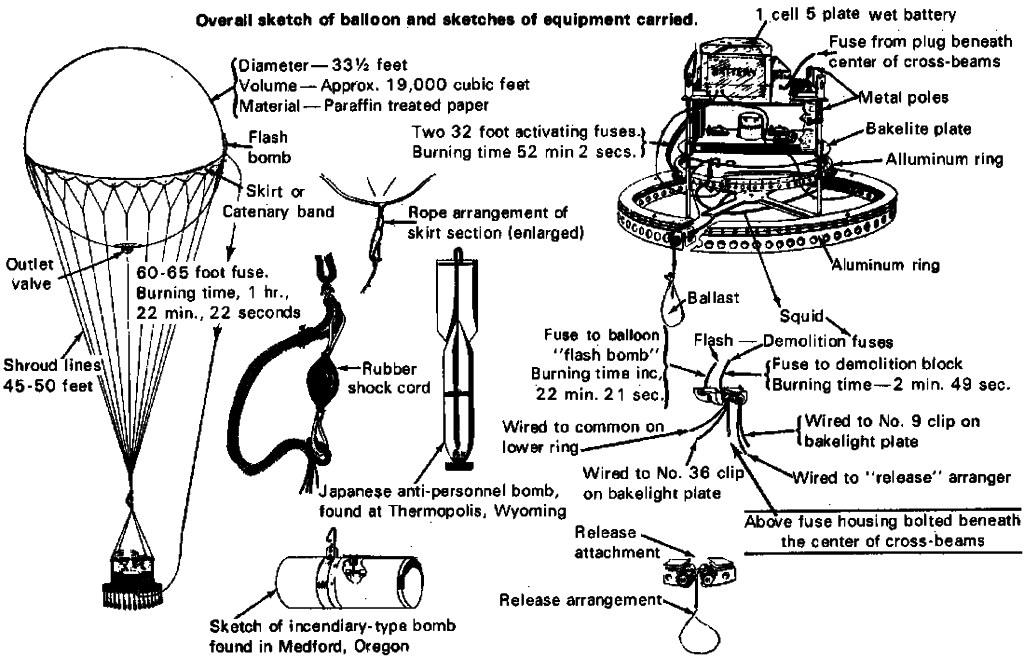
Figure 2. A number of onboard subsystems automatically controlled the Fu-Go balloon’s altitude to keep it in the jet stream, release its incendiaries upon arrival, and then cause the entire configuration to self-destruct.
From the very beginning, military applications for unmanned systems were eagerly pursued in hopes of obtaining government funds for both development and future sales. In the maritime domain, the precursor to unmanned surface vehicles (USVs) was the fire ship, a vessel of opportunity loaded with combustible materials and set afire to bear down upon the enemy, driven by prevailing winds and tides. Its Achilles heel was the unpredictable trajectory of the burning hulk (which could reasonably be outmaneuvered unless the target ships were at anchor), compounded by the inherent lack of surprise. Remote control offered obvious advantages, and applying such a solution to a boat in two dimensions was far more forgiving than doing so with an airship in three.
Accordingly, in 1862, Captain W.H. Noble of the Royal Navy proposed (but never pursued) an electrically steered surface craft as a means for guiding a fire ship toward an enemy fleet. Just 2 years later, Captain Giovanni Luppis of the Austrian Navy unsuccessfully approached British civil engineer Robert Whitehead about steering an unmanned spar-torpedo boat, using long ropes from shore to control the rudder. The first practical demonstration of a remotely guided unmanned surface vehicle has its origins in an 1870 design proposed by a Prussian artillery officer named Werner Siemens (Figure 3), to be pneumatically steered via a trailing air hose.
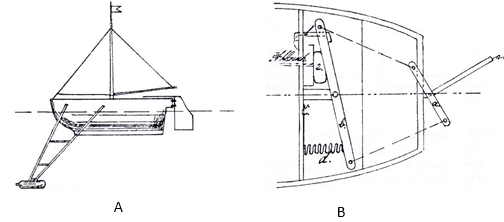
Figure 3. A) Elevation view of the remote-controlled sailboat, armed with a spar torpedo, as proposed by Werner Siemens in 1870. B) Plan view of the pneumatically actuated tiller mechanism, controlled by varying the pressure in rubber bag e via a trailing air hose (not shown).
Soon to be the founder of a huge industrial conglomerate that would bear his name, Siemens constructed a far more practical working prototype just two years later, which by 1874 could be electrically controlled via a single-conductor tether, the return circuit being through the seawater. Rudder deflection of the steam powered vessel was achieved using polarized relays (invented by Siemens) and reversing the control current on shore (Figure 4), with the rudder returning amidships whenever the current ceased. In the absence of operator input, the innovative remote steering mechanism even provided for automatic heading stabilization, based upon an onboard magnetic compass.
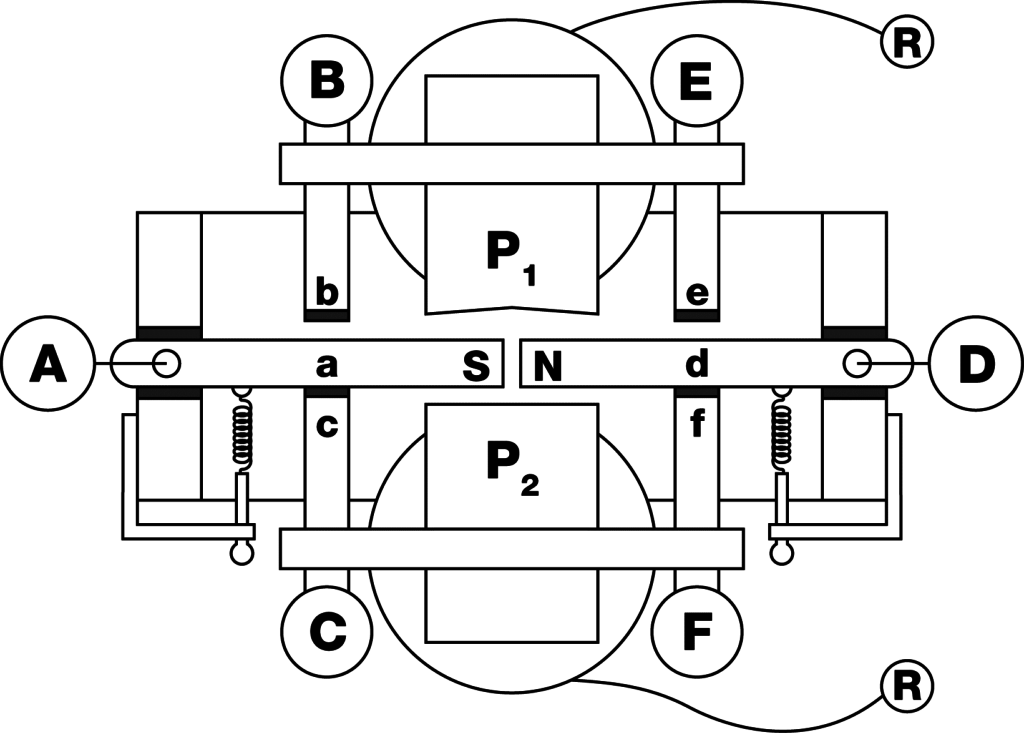
Figure 4. A typical polarized-relay configuration employed a pair of permanent-magnet armatures a and d to actuate either of two sets of electrical contacts a-b-c or d-e-f, depending on the direction of the coil current flowing between binding posts R.
The most significant nineteenth century USV was developed by Nikola Tesla, a Serbian immigrant to the United States, and one of the most prolific inventors of all time. In 1897, he constructed a radio-controlled “telautomaton” in the form of a boat (Figure 5), which was privately demonstrated for investors at the first Electrical Exposition at Madison Square Garden in September of the following year. Tesla’s pioneering work was significant for two reasons: 1) it appears to have been the first reduction to practice of a radio-controlled unmanned system; and, 2) it provided effective means of such radio control over multiple subsystems via multiplexing, versus a single binary on-off function.
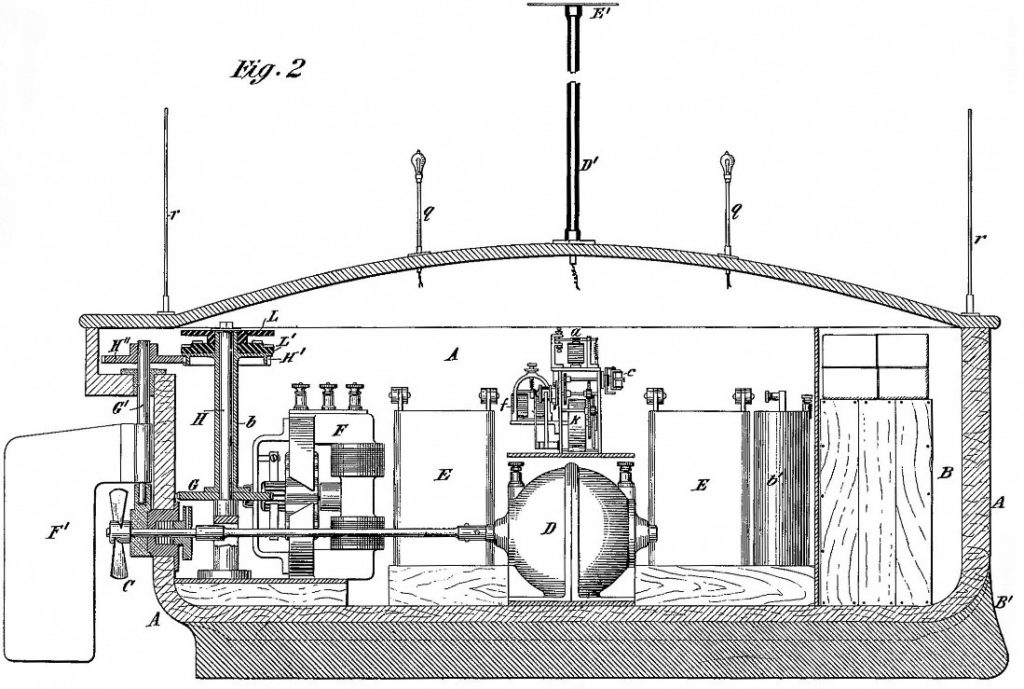
Figure 5. Tesla’s radio-controlled boat, approximately 4 feet long by 3 feet high, employed a series of storage batteries E to power propulsion motor D and steering motor F (adapted from US Patent No. 613,809).
But in 1897, some seven years prior to the invention of even the most simplistic “diode-valve” vacuum tube by Professor Ambrose Fleming in 1904, how was radio-control even possible? The answer traces back to an unusual but simplistic component devised by the French physicist Edouard Branly, who published his findings in 1890. The subject device consisted of a small glass tube, filled with metal filings and capped at both ends by conductive plates, which came to be known known as a “filings tube.” In 1894, the English physicist Oliver Lodge demonstrated an application of Branly’s filings tube as a mechanical radio-frequency (RF) detector, which he called a “coherer.” It would prove to be a huge technological innovation that ushered in a whole new era of possibilities.
The secret to the coherer’s success as an RF detector was Branley’s observation that the metal filings inside the non-conductive tube tended to clump together (or cohere as Lodge put it) in the presence of an RF signal, causing the impedance across coherer terminals A and B in Figure 6 to decrease significantly. In essence, the coherer was an RF-actuated single-pole switch. In practice, the broad-band RF signal from a spark-gap transmitter was received by the antenna at upper left and passed to ground through coherer C. The resulting impedance drop increased the current flow from battery B1 through the coil of sensitive relay R, drawing in the relay armature to close its contacts, thereby allowing battery B2 to activate power relay S for the control output.
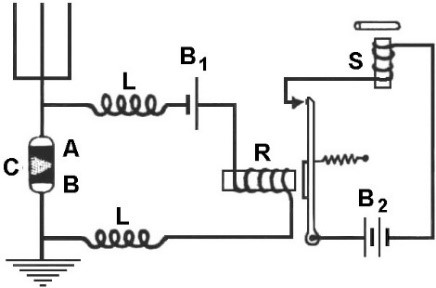
Figure 6. Schematic diagram of an 1896 Marconi receiver design using coherer C as an RF detector (decohering clapper not shown), forming a binary on-off controller via electrical relays R and S.
The fly in the ointment was that once clumped together by the RF signal, the metal filings inside the coherer tended to stay clumped even after the RF signal ceased, meaning neither relays R or S would drop out. To get around this problem, an electromechanical clapper (typically a doorbell without the bell) was wired in parallel with relay S, and positioned so as to vibrate the coherer assembly and shake loose the filings. (As long as an RF signal was being received, the metal filings remained cohered.) Besides being the first to apply radio control to an unmanned vehicle, Tesla’s further contribution was to demultiplex multiple commands from the received binary pulse train, such as start, stop, reverse, turn left, or turn right.
That same year, Englishmen Ernest Wilson and C.J. Evans reportedly operated slow moving boats on the Thames River using a coherer-based radio-receiver design that controlled steering only. Lacking Tesla’s multiplexing scheme, they instead used two separate transmitters and receivers for deflecting the rudder either left or right, with two orthogonal antenna dipoles to achieve signal discrimination (Figure 7). On March 26, 1898, the pair received UK patent No. 7,382 entitled “Improvements in Methods of Steering Torpedoes and Submarine Boats,” and US Patent No. 663,400 entitled “Methods of Controlling Mechanisms by Means of Electric or Electromagnetic Waves of High Frequency” on December 4, 1900.
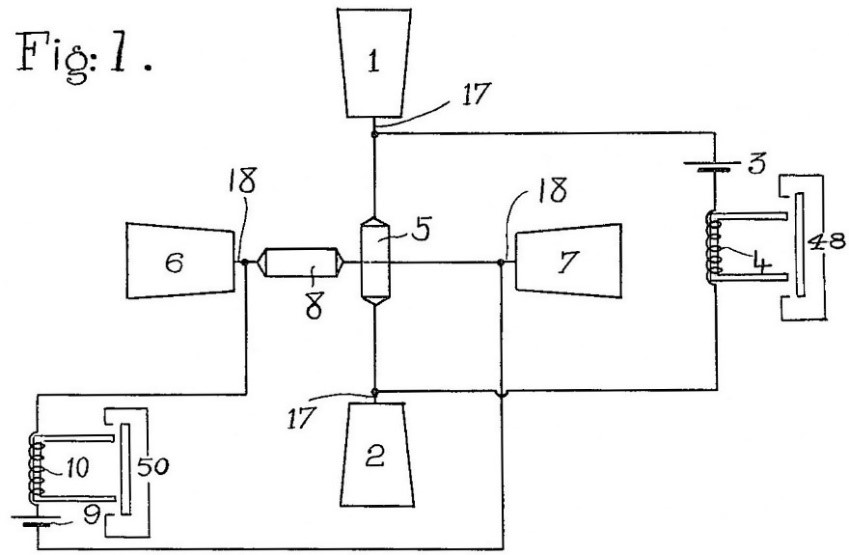
Figure 7. The radio-control scheme of E. Wilson and C.J. Evans employed two separate receivers with their antenna pairs 1-2 and 6-7 arranged orthogonally (i.e., one vertical and one horizontal) for two-channel selectivity (redrawn from US Patent No. 663,400).
Note the proposed military application of remote torpedo guidance in the UK patent title, which was a topic of considerable interest around the turn of the century. Having viewed the previously mentioned concept for a shore-guided surface craft proposed by Captain Giovanni Luppis in 1864 to be impractical, British engineer Robert Whitehead had developed instead a cylindrical torpedo driven by compressed air, completed in 1866. Lacking gyro stabilization, this forerunner of modern torpedoes suffered from poor accuracy, for which wire-guided and later radio-control solutions seemed to offer great promise. A plethora of attempts to create practical dirigible (steerable) torpedoes, both wire-guided and wireless, were soon undertaken by inventors all over the world.
The first such device to become an actual service weapon was conceived by a Union naval officer named John Lewis Lay, who had developed the Wood-Lay spar torpedo during the American Civil War. The term torpedo originally denoted what is now more commonly called a mine, essentially a floating or submerged explosive device that detonated when struck by a ship, or was remotely triggered via an electric cable from shore. Having resigned his commission after the war, Lay was hired to design the underwater defenses of Callao, Peru, in preparation for an anticipated Spanish attack. While thus engaged laying down a submerged defensive network of electrically fired torpedoes (i.e., anchored mines), Lay was struck by a sudden inspiration.
The “torpedo planter” in which he was embarked carried a torpedo attached to a reel of insulated wire, and as the small boat advanced, this trailing wire leading back to shore was paid out by rotating the reel. Lay reasoned that if the boat were provided with motive power, he could remotely control it from shore with electrical signals sent over the trailing wire. In this way, the torpedo could seek out an enemy vessel, instead of waiting to be hit by one. Furthermore, a cylindrical “auto-mobile” (self-powered) torpedo that ran beneath the surface was an even better delivery option than an exposed boat.
Upon completion of his Peruvian venture in 1867, Lay returned to his hometown of Buffalo, NY, to pursue his idea. Key innovations were: 1) remote electrical steering via polarized relays and a single-conductor tether; and, 2) propulsion from expanding pressurized carbonic acid (H2CO3) from its liquid to gaseous state (CO2). This approach, suggested in 1869 by Walter Hill of the Naval Torpedo Station, yielded more potential energy for the same size storage flask than the compressed air used in Whitehead’s torpedo. While Lay’s first two prototypes proved impractical (Figure 8), he successively improved the design in 30 subsequent iterations over the next 20 years, filling orders from the United States, Egypt, Peru, and Russia.
Figure 8. Lay Torpedo No. 2 at the Naval Torpedo Station, Newport, RI, circa 1892, where it was known as Station Lay No. 1, or as marked here, Lay Torpedo No. 1 (US Navy photo).
Meanwhile, inspired by the dangers associated with his dirigible-airship attempts in the late nineteenth century, the Spanish inventor Leonardo Torres-Quevedo sought a more practical means for wireless development, using a test surrogate in a marine environment. The very first Telekino prototype, however, was a portable mock-up, a large wooden box fitted with a propeller and rudder, which he presented to the Academy of Sciences in Paris on August 3, 1903. This surviving assembly, now almost 115 years old, is on display at the Torres-Quevedo Museum at the Civil Engineering Faculty of the Polytechnic University of Madrid (Figure 9).
Figure 9. The original Telekino feasibility-demonstration hardware on display at the Torres-Quevedo Museum at the Civil Engineering Faculty of the Polytechnic University of Madrid (courtesy Antonio Perez-Yuste).
The Telekino control circuitry expanded upon Tesla’s earlier distributor design by increasing the number of rotary-switch positions, and providing separate encoder disks for propulsion and steering (Figure 10). Decoder disk H was used to select one of five possible propeller speeds, including stop, whereas disk T provided five preset helm positions either side of “rudder amidships.” Interestingly, Torres-Quevedo chose to conduct initial Telekino testing of this maritime surrogate for his envisioned dirigible airship on a surrogate of its own, in the form of a three-wheeled land vehicle. Unfortunately, no pictures of the latter are known to exist.
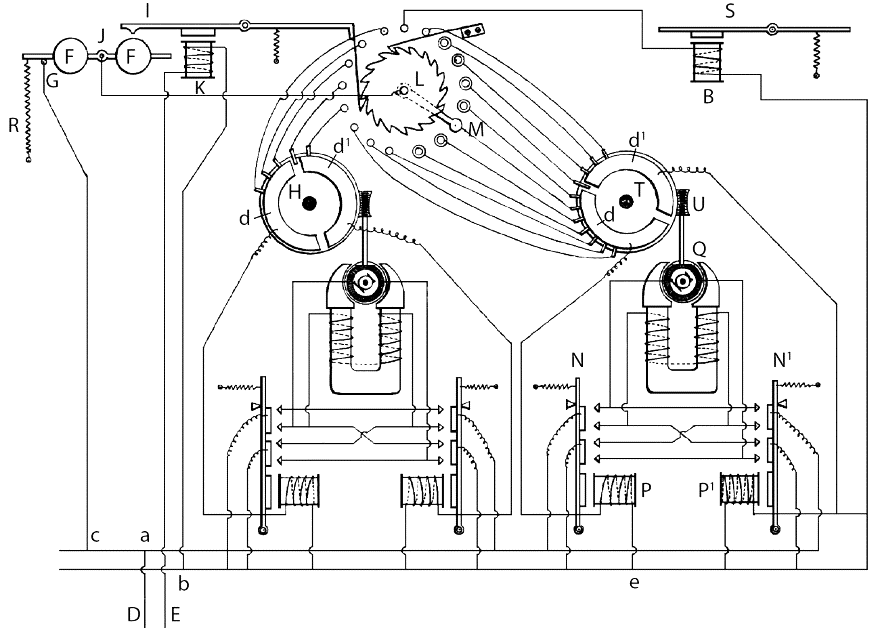
Figure 10. The Telekino employed two motor-driven decoder disks H (propulsion) and T (steering), which were positioned in response to the output of a rotary switch, which was incremented by ratchet-and-pawl mechanism L in response to pulses detected by the receiver (redrawn from Spanish Patent No. 33,041).
In 1904, preliminary experiments using a small electric boat were run at the Royal Country House Lake in Madrid, with a maximum control range of about 250 meters. The next demonstration, using the electrically powered launch Vizcaya, took place in the Estuary of Bilbao near Algorta on March 5, 1905, followed by a well-advertised public demonstration in the port of Bilbao on November 7 (Figure 11). An impressive standoff range of 2 kilometers was achieved, witnessed by a very large and enthusiastic crowd of attendees. Unable to obtain further support from the Spanish government, however, Torres-Quevedo abandoned all further pursuit of radio control.
Figure 11. The rather bulky Telekino apparatus, similar to that shown in Figure 9, has just been relocated from the dock to the stern of Vizcaya at Abra de Bilbao, 6 September 1906 (courtesy www.torresquevedo.org).
The previously mentioned three-wheeled test surrogate employed by Torres-Quevedo in 1904, which had an effective range of just 20 to 30 meters, appears to be the first known example of a radio-controlled unmanned ground vehicle (UGV). Practical military applications in the ground domain did not come into play until WWI, spurred by the devastating stalemate of trench warfare. At least two tethered UGVs were introduced by the French in 1915. The wire-guided Crocodile Schneider Torpille Terrestre (Figure 12a) carried a 40-kilogram internal charge for attacking German barbed-wire and concrete-casement defenses. Its lackluster performance during operational testing through June, 1916 was eclipsed by higher expectations for the newly introduced battle tanks.
Figure 12. A) Several Crocodile Torpille Terrestre (Type B) land torpedoes are lined up outside the Schneider plant in Le Creusot, France. B) The French Aubriot-Gabet Torpille Electrique land torpedo featured a third track angled upward at front center, probably to flatten barbed-wire defenses. (Ministere de la Guerre photos.)
The similar Aubriot-Gabet Torpille Electrique explosive charge carrier was powered by a single electric motor mounted on its upper rear deck (Figure 12b). This instantiation appears to be unsteerable, which was in keeping with the nature of its intended target, the nearby and very long opposing trenches of the enemy. The trailing tether was described in a postwar article in Scientific American as providing power for the drive motor and being paid out from the vehicle, versus dragged over the ground. While both the Torpille Terrestre and the Torpille Electrique were reportedly tested in battle but never series produced, they nonetheless set the stage for numerous improved UGVs that would see extensive use in WWII.
About the Author
Commander (Ret.) H.R. (Bart) Everett is the former Technical Director for Robotics at the Space and Naval Warfare Systems Center Pacific in San Diego, CA. In this capacity he has served as Technical Director for the Idaho National Laboratory (INL) Advanced Unmanned Systems Development Program funded by the Office of the Secretary of Defense (OSD), Technical Director for the Army’s Mobile Detection Assessment Response System (MDARS) robotic security program, and chief engineer for the USMC Ground Air Robotic System (GATORS). He is the former Director of the Office of Robotics and Autonomous Systems (SEA-90G), Naval Sea Systems Command, Washington, DC, and has been active in the field of robotics for over 50 years, with personal involvement in the development of over 40 mobile robotic systems, with an emphasis on sensors and autonomy. He has published more than 125 technical papers and reports (including several books), and has 21 related patents issued or pending. He serves on the Editorial Board for Robotics and Autonomous Systems magazine and is a member of AUVSI, IEEE, and Sigma Xi. This article draws from his book, Unmanned Systems of World Wars I and II, MIT Press, 2015. Find him on Twitter: @HRBartEverett
